This article originally appeared in The Skeptic, Volume 4, Issue 2, from 1990.
Observers of the paranormal will frequently find themselves challenged by arguments along the lines of: ‘Such a coincidence could never have happened by chance – there must be some other explanation’ applied to surprising happenings of one sort or another.
In this article I will bring out two principles, both of which lead people greatly to underestimate the likelihood of ‘coincidences’. An understanding of these principles is indispensable in any attempt to examine the weight to be given to arguments of the above type.
The discussion is from a statistical point of view, but should be accessible to non-statisticians.
PRINCIPLE no. 1: People generally underestimate the chance of a coincidence, even in straightforward situations.
The principle is nicely illustrated by a familiar (to first year statistics students) puzzle usually referred to as ‘The Birthday Problem’. The BP concerns itself with the probability of getting coincidences of birthdays amongst a randomly selected group of people. This is a straightforward probability calculation about which there is no mystery, except that the answer is found to be surprising. Test your intuition on the following question:
The Birthday Problem: How large a random group of people do your need to take in order to have a 50% chance that there will be at least one coincidence of birthdays in the group? Don ‘t read further – stop and guess how big the group should be. Obviously a group of size 366 would give certainty of a coincidence, because there are only 365 possible birthdays (ignoring 29 Feb). By contrast, a group of size 2 only gives you a chance of 1 in 365 that the two have the same birthday. So somewhere between 2 and 366 is the correct answer.
The surprise is that the answer is 23. This is probably a smaller number than you guessed. Most people guess higher than 40 or sometimes higher than 100. For completeness here are some figures:
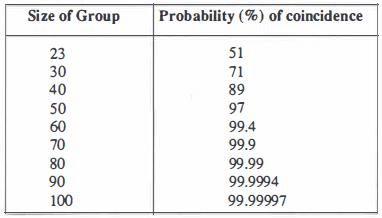
So you can see that with 50 people there is only a 3% chance that you don’t find a coincidence, and with 100 people there is a chance of only 3 in 10 million of no coincidence (i.e. all have different birthdays).
The point is that most people greatly underestimate the probability of a simple coincidence.
The above reasoning is generally true – there is nothing special about birthdays – they just happen to be convenient examples of uniform random quantities. Similar arithmetic applies if you randomly generate numbers, for example on a roulette wheel, or observe other random quantities.
People sometimes ask how the answer (23) can be correct. The arithmetic is certainly correct, but perhaps the following way of thinking will help explain how it comes to be: consider the converse – i.e. birthdays all being different. Imagine you have a calender on the wall with all the days in succession (e.g. by throwing darts blindfolded). What odds would you be prepared to lay that he would hit 23 different days? For the first few you might feel safe, but you would start becoming aware of the mounting odds of a coincidence as each successive dart would have a larger number of already selected days that it might hit. Fair odds would be about 50%.
Try the experiment yourself next time you have 22 or so random (?!) people in the room with you.
PRINCIPLE no 2: The mind is a much better a positeriori pattern recogniser than we realise.
In principle no 1 we talked about the probability of some a priori (from beforehand) specified event. In this principle we turn our mind to ‘coincidences’ that we weren’t thinking about a priori, but looking back from afterwards (a posterioi) we notice have happened.
Whenever I give a talk about the Birthday Problem, I also announce that some surprising coincidence (which I am careful not to specify) will emerge when we do an actual birthday test on the audience. These are some of the things that have happened on different occasions:
- Identical twins were in the audience
- It was someone’s birthday that day
- The first birthday called out hit a match
- The two people with the same birthday were sitting next to each other
- The matching birthday found was also the date of the Windhoek air disaster. (According to a third member of the audience)
Here are some of the things that haven’t occurred (yet):
- The first birthday called out is 1 January
- Some sort of sequence e.g. 7, 8, 9 February or 1 January, 1 February, 1 March
- Somebody doesn’ t know their true birthday
- Somebody has two birthdays (registration error)
I hope these examples give you the idea: there are a huge number of events that we don’t ever consciously think about until after they have happened; then we suddenly think of them a posteriori as having been very unlikely. ‘What is the probability that when you do a birthday test you find twins in the audience? ‘-well, admittedly this is small, but the question is misleading. It should have been ‘What is the probability of twins or some other more or less similarly surprising event?’. Now, the answer is ‘pretty high’. I can’t be more specific because the list of ‘similarly surprising’ events is rather long and vague, as the examples above have probably conveyed.
The lesson is that the mind can find patterns in randomness, thereby misleading one ‘s subjective assessment of how surprising (and therefore inexplicable) some event is. The mind automatically picks up the occurrences of coincidences but never accounts the non-occurrences (from the long, vague list of these) thus giving a biased picture. Everyone has a favourite story about some ‘incredible’ coincidence that happened to them, but would be hard pressed to list all the incredible coincidences that didn’t happen. After all, 1 in a million chances do occur – about once every million times. Because your mind so effortlessly notices a surprising pattern, you never get to notice the 999,999 non-occurences of other patterns.
I hope these two principles (there are more!) will forearm you in the critical appraisal of the evidence lent by ‘coincidences’.



