The proclamation “extraordinary claims require extraordinary evidence” was oft spoken by American astronomer and science communicator Carl Sagan. He was not the first to express some version of the sentiment, but definitely popularised that particular phrase.
Is this a mere platitude or is Sagan making a valid point? The answer hinges on what is meant by “extraordinary”. There are many dimensions that could be used to measure the extraordinariness of a claim. It could be the novelty, the utility, or the complexity of a claim that make it extraordinary. None of these features would necessarily alter the strength of evidence needed to affirm that claim.
What Dr Sagan meant by “extraordinary” was a claim that is highly unlikely or implausible. In that context, the essence of Sagan’s statement is valid. If a particular strength of evidence is just persuasive enough to validate a claim, a less plausible claim would require stronger evidence to achieve the same threshold. An extraordinary claim would lie at the far extreme of implausibility.
We apply this principle constantly, but mostly unconsciously, in our daily lives. If a colleague shows up late to work and attributes their delayed arrival to a traffic jam, we would not give it a second thought. If the same coworker attributed their tardiness to an alien abduction, we would be much less charitable. In both examples, our coworker is providing the same quality of evidence, a personal testimonial. Why is this level of evidence sufficient to accept one claim but not the other? Traffic is a mundane, highly plausible event. Based on what we know of the world, alien abduction is much less common and much less plausible than heavy traffic.
Let’s do a thought experiment to understand the interplay between the plausibility of a claim and the persuasiveness of the evidence.
Here are the assumptions for this thought experiment.
- Our protagonist is “Homer”. Homer is frequently late for work.
- There are only two possible reasons for Homer’s late arrival to work: heavy traffic or alien abduction.
- Heavy traffic is responsible for 98% of Homer’s late arrivals and alien abductions are responsible for 2%.
- Despite his unreliable arrival, Homer is a pretty honest reporter. He accurately attributes the true cause for his late arrival 95% of the time and inaccurately reports the alternate excuse 5% of the time. In other words, his testimonial is accurate 19 out of 20 times and inaccurate for 1 out of 20 late arrivals. Not perfect, but mostly correct.
You are Homer’s Human Resources manager. Late arrivals due to traffic are not excused, but late arrivals due to alien abduction are excused because they are considered “acts of nature”. Given that he reports the correct excuse 95% of the time, you can accept the fact that 19 out of 20 times he reports alien abduction, he is doing so accurately, right?
Let’s run a simulation of 1,000 late arrivals and see.
For the 1,000 late arrivals, 98% or 980 will be due to traffic and 20 will be due to aliens. For the traffic delays, 95% of the time (931 of 980) Homer will accurately report the cause as “traffic” and 5% (49/980) he will inaccurately report as “aliens.”
For clarity, we can enter the results into a table.

For the 20 alien abductions, Homer will correctly report 95% (19 of 20) as “aliens” and incorrectly report one as “traffic”. Add this as another row to the table. The green cells represent the events for which Homer’s excuse matches reality. The red cells represent the events for which Homer’s excuse does not match reality.
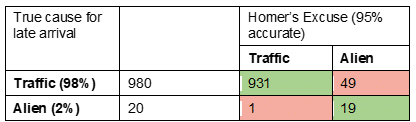
If we sum the contents of the green cells: 931 + 19 = 950, this confirms that Homer correctly reported the cause of his tardiness 95% of the time. The sum of the green cells is 49 + 1 = 50, confirming that Homer incorrectly reported the cause of his tardiness 5% of the time.
If we sum the columns on the right half of the table, we can determine the number of times Homer reported “Traffic” and the number of times he reported “Aliens.”
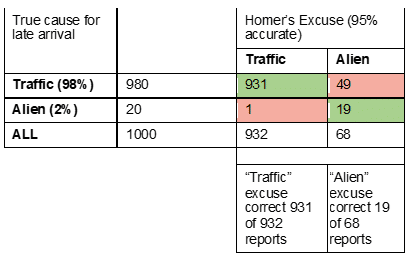
On Monday, Homer is late, and reports “traffic” as the excuse. The table tells us that for every 932 times Homer reports traffic, his report is correct 931 times. A traffic excuse accurately reflects reality 99+% of the time.
On Friday, Homer is late again and reports “alien” as his excuse. For every 68 times Homer reports aliens, his excuse is correct only 19 times. A report of alien abduction accurately reflects reality only 28% of the time.
If Homer is 95% reliable overall, why this inconsistency for traffic and alien abductions? The 5% inaccurate reports are not distributed symmetrically. The mundane “traffic” events generate a disproportionate number of false “alien” excuses.
In this model we could consider a report of “traffic” an ordinary claim, and evidence with 95% reliability ordinary evidence. This combination leads to a correct conclusion over 99% of the time.
We could consider “alien abduction” an extraordinary claim. The same ordinary evidence leads to a correct conclusion only 28% of the time. In order to have confidence that Homer’s extraordinary reports of alien abduction we would need some form of evidence with greater than 95% reliability.
Like any model, our thought experiment has limitations. The example used presents a binary choice between two mutually exclusive claims. The frequencies of the two claims are known and are constant: 98% traffic and 2% aliens. We also have a known accuracy of the evidence, and the accuracy is the same for both contingencies; Homer’s excuse is 95% accurate for traffic events and 95% accurate for alien events. These levels of precision and consistency are unrealistic in the real world, but instructive in our model.
We can run variations of the model with different frequencies of the 2 excuses, and different degrees of reliability in Homer’s reporting. If we make alien abductions less than 2% likely (more extraordinary), Homer’s reports of alien abduction become even less reliable reflections of reality.
The only version of this model for which ordinary and extraordinary claims have equal evidentiary value is a model in which Homer is a perfect reporter, accurately attesting the cause of his late arrival 100% of the time. In that universe every claim, no matter how implausible, could be accepted at face value.

In the real world, evidence is not perfect. The plausibility of a claim is not accurately known. The relative plausibility of competing claims can be quite contentious. Despite these confounding factors, the principle expressed by Dr Sagan is worth remembering.
If I were to expand to a more nuanced version of Sagan’s dictum, it would go something like this: The strength of the evidence required to accept a claim should be adjusted in proportion to the implausibility of the claim. The more implausible claim, the stronger the evidence required to accept that claim.



